13. 라플라스(Laplace) & Z 변환(Z-transform) 변환표(Conversion table)

 

라플라스(Laplace) & Z 변환(Z-transform) 변환표(Conversion table)

시간 함수로 표현 되는 연속 시스템 함수 f(t)의 라플라스로 변환된 함수 F(s)와 등가 디지털 신호인 이산 신호 f(kT) 그리고 Z 변환된 함수 F(z)의 관계에 따른 변환표이다.

라플라스(Laplace) 변환표(Conversion table)

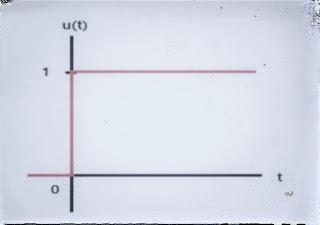
시간 t가 0 이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환하면 \(\frac{1}{s}\)가 된다.

\[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \]

이처럼 계단 함수(Step function)는 라플라스 정의에 따라 \(\frac{1}{s}\)가 된다.

\[ \begin{align} L[u(t) &= \int_0^\infty u(t) e^{-st}dt = \int_0^\infty 1 \cdot e^{-st}dt \\[12pt] &= \left[\frac{e^{-st}}{-s} \right]_0^\infty = \frac{1}{s} \end{align} \]

계단 함수 u(t)는 시간에 따라 표현 되는 시간 함수이고 계단 함수를 라플라스 변환하면 \(\frac{1}{s}\)가 된다. 
시간 함수를 f(t)로 라플라스 함수는 F(s)로 나타낸 테이블이다.

No.	\[f(t)\]	\[F(s)\]
1	\[1(t)\]	\[\frac{1}{s}\]
2	\[t^n, \ \ n>0\]	\[\frac{n!}{s^{n+1}}\]
3	\[e^{-at}\]	\[\frac{1}{s+a}\]
4	\[te^{-at}\]	\[\frac{1}{(s+a)^2}\]
5	\[1-e^{-at}\]	\[\frac{a}{s(s+a)}\]
6	\[sin\omega t\]	\[\frac{\omega}{s^2+\omega^2}\]
7	\[cos\omega t\]	\[\frac{s}{s^2+\omega^2}\]
8	\[e^{-at}sin\omega t\]	\[\frac{\omega}{(s+a)^2+\omega^2}\]
9	\[e^{-at}cos\omega t\]	\[\frac{s+a}{(s+a)^2+\omega^2}\]
10	\[\delta(t)\]	\[1\]
11	\[f(t-\theta)\]	\[e^{-\theta s}\]

Z 변환(Z-transform) 변환표(Conversion table)

연속 시간 함수를 일정 주기로 표본화하면 이산 시간 신호를 얻을 수 있다. 
여기에서 표본화는

\[ f(t) = \sum_{k=0}^{\infty} f(t) \delta(t-kT) \]
으로 표현한다.

계단 함수를 Z 변환으로 바꾸면 등비수열 형태로 나타난다.

\[ \begin{align} F[z] = Z[f(k)] = \sum_{k=0}^{\infty} z^{-k} &= 1 + z^{-1} + z^{-2} + \cdots \\[12pt] &= \frac{1}{1-z^{-1}} \end{align} \]

함수 f(k)를 Z-변환하면 \( \frac{1}{1-z^{-1}} \)이다. 이처럼 이산신호는 Z-변환된 함수로 나타낼수 있다.
이산 신호 f(kT)를 Z 변환 함수는 F(z)로 나타낸 테이블이다.

No.	\[f(kT)\]	\[F(z)\]
1	\[1(k)\]	\[\frac{1}{1-z^{-1}}\]
2	\[kT\]	\[\frac{Tz^{-1}}{(1-z^{-1})^2}\]
3	\[e^{-akT}\]	\[\frac{1}{1-e^{-aT}z^{-1}}\]
4	\[kTe^{-akT}\]	\[\frac{Te^{-aT}z^{-1}}{(1-e^{-aT}z{-1})^2}\]
5	\[1-e^{-akT}\]	\[\frac{(1-e^{-aT})z^{-1}}{(1-z^{-1})(1-e^{-aT}z^{-1})}\]
6	\[sin\omega kT\]	\[\frac{z^{-1}sin\omega T}{1-2z^{-1}cos\omega T+z^{-2}}\]
7	\[cos\omega kT\]	\[\frac{1-z^{-1}cos\omega T}{1-2z^{-1}cos\omega T+z^{-2}}\]
8	\[e^{-akT}sin\omega kT\]	\[\frac{e^{-aT}z^{-1}sin\omega T}{1-2e^{-aT}z^{-1}cos\omega T+e^{-2aT}z^{-2}}\]
9	\[e^{-akT}cos\omega kT\]	\[\frac{1-e^{-aT}z^{-1}cos\omega T}{1-2e^{-aT}z^{-1}cos\omega T+e^{-2aT}z^{-2}}\]
10	\[\delta(k)\]	\[1\]
11	\[f(n-k)\]	\[z^{-k}\]

 

라플라스와 Z 변환 변환표

시간 함수 f(t), 라플라스 함수 F(s), 이산 신호 f(kT) 그리고 Z 변환된 함수 F(z)의 변환표이다.

No.	\[F(s)\]	\[f(t)\]	\[f(kT)\]	\[F(z)\]
1	\[\frac{1}{s}\]	\[1(t)\]	\[1(k)\]	\[\frac{1}{1-z^{-1}}\]
2	\[\frac{1}{s^{2}}\]	\[t\]	\[kT\]	\[\frac{Tz^{-1}}{(1-z^{-1})^2}\]
3	\[\frac{1}{s+a}\]	\[e^{-at}\]	\[e^{-akT}\]	\[\frac{1}{1-e^{-aT}z^{-1}}\]
4	\[\frac{1}{(s+a)^2}\]	\[te^{-at}\]	\[kTe^{-akT}\]	\[\frac{Te^{-aT}z^{-1}}{(1-e^{-aT}z{-1})^2}\]
5	\[\frac{a}{s(s+a)}\]	\[1-e^{-at}\]	\[1-e^{-akT}\]	\[\frac{(1-e^{-aT})z^{-1}}{(1-z^{-1})(1-e^{-aT}z^{-1})}\]
6	\[\frac{\omega}{s^2+\omega^2}\]	\[sin\omega t\]	\[sin\omega kT\]	\[\frac{z^{-1}sin\omega T}{1-2z^{-1}cos\omega T+z^{-2}}\]
7	\[\frac{s}{s^2+\omega^2}\]	\[cos\omega t\]	\[cos\omega kT\]	\[\frac{1-z^{-1}cos\omega T}{1-2z^{-1}cos\omega T+z^{-2}}\]
8	\[\frac{\omega}{(s+a)^2+\omega^2}\]	\[e^{-at}sin\omega t\]	\[e^{-akT}sin\omega kT\]	\[\frac{e^{-aT}z^{-1}sin\omega T}{1-2e^{-aT}z^{-1}cos\omega T+e^{-2aT}z^{-2}}\]
9	\[\frac{s+a}{(s+a)^2+\omega^2}\]	\[e^{-at}cos\omega t\]	\[e^{-akT}cos\omega kT\]	\[\frac{1-e^{-aT}z^{-1}cos\omega T}{1-2e^{-aT}z^{-1}cos\omega T+e^{-2aT}z^{-2}}\]
10	\[1\]	\[\delta(t)\]	\[\delta(k)\]	\[1\]
11	\[e^{-\theta s}\]	\[f(t-\theta)\]	\[f(n-k)\]	\[z^{-k}\]

※ No. 2의 n=1.