22. Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임((Integrator with first order and dead time)


Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임(Integrator with first order and dead time)


Integrator with first order and dead time, Laplace 모델의 Z 변환은 역변환된 시간함수로 구한다.

\[ f(t)=f(t-θ)\frac{1}{τ_1} \left(1-e^{-\frac{τ_1}{τ_2}  t}\right) \]



적분과 데드타임으로 이루어진 1차 함수의 Z 변환과 특성


위의 역변환된 시간함수를 라플라스 & Z 변환표를 참조하여 변환한다.

\[ δ(n-k)  → Z→ Z^{-k} \]

\[ 1(k)  → Z→  \frac{1}{1-z^{-1} } \]

\[ e^{-akT}  → Z→  \frac{1}{1-e^{-aT} z^{-1}}  \]

δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}\)의 a는 \(\frac{τ_1}{τ_2}\) T이다.

\[ \begin{align} F(z)&= z^{-θ} \frac{1}{τ_1}  \left(\frac{1}{1-z^{-1}}-\frac{1}{1-e^{-\frac{τ_1}{τ_2} T}  z^{-1}}\right)\\[12pt]&= z^{-θ}  \frac{1}{τ_1} \left\{\frac{(1-e^{-\frac{τ_1}{τ_2} T}  z^{-1} )-(1-z^{-1} )}{(1-z^{-1} )(1-e^{-\frac{τ_1}{τ_2}  T}  z^{-1} } \right\}\\[12pt]&= z^{-θ} \frac{1}{τ_1}  \left\{\frac{(-e^{-\frac{τ_1}{τ_2} T}+1) z^{-1}}{1+(-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-1}+e^{-\frac{τ_1}{τ_2}  T}  z^{-2} }\right\}\\[12pt]&=\frac{\frac{1}{τ_1}  (-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-θ-1}}{1+(-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-1}+e^{-\frac{τ_1}{τ_2}  T}  z^{-2} } \end{align} \]

이것을 차분 방정식 형태로 표기하자

\[ F(z)=\frac{Output(zero-state response)}{Input}=\frac{Y(z)}{X(z)}\]

\[(Input)Y(z)=(Output)X(z)\]

\[ \begin{align} &\left\{1+\left(-e^{-\frac{τ_1}{τ_2}  T}+1\right) z^{-1}+e^{-\frac{τ_1}{τ_2}  T}  z^{-2} \right\}Y(z)\\[12pt]&=\left\{\frac{1}{τ_1}  \left(-e^{-\frac{τ_1}{τ_2} T}+1\right) z^{-θ-1} \right\}X(z) \end{align} \]

좌측 수식은 y[k]에 해당하며 이것을 기준으로 정리한다.

\[ \begin{align} y[k]=&-\left(-e^{-\frac{τ_1}{τ_2}  T}-1\right)\cdot y[k-1]\\[12pt]&-e^{-\frac{τ_1}{τ_2} T}\cdot y[k-2]\\[12pt]&+\frac{1}{τ_1} (e^{-\frac{τ_1}{τ_2}  T}+1)\cdot f[k-θ-1] \end{align} \]

θ=0, 표본주기 T=0.1 그리고 τ에 따라 아래와 같은 응답특성을 보인다. 

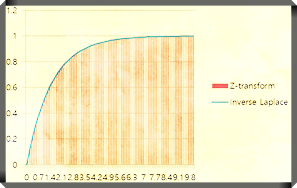τ1=1, τ2=1.5, Integrator first order of Z-transform
τ1=1, τ2=1.5, Integrator first order of Z-transform


τ1=2, τ2=1, Integrator first order of Z-transform
τ1=2, τ2=1, Integrator first order of Z-transform


Z 변환을 통한 특성과 Laplace 역변환을 통한 응답특성은 동일하다.


댓글

댓글 쓰기

이 블로그의 인기 게시물

1. 라플라스 변환과 Z 변환(Laplace transform and Z-transform)

이미지
라플라스 변환 (Laplace transform) 함수 f(t)에 \( e^{-st} \)를 곱해 t=0에서 t=∞까지 t에 대해 적분하였을 때, 적분값이 존재하는 경우에는 s에 관한 함수로 표현되며 s에 대한 새로운 함수를 함수 f(t)의 라플라스 변환(Laplace transform)이라고 한다. 이를 수식으로 표현하면 다음과 같다. \[ F(s)=L[f(t)]=\int_{0+}^\infty e^{-st} f(t)dt \] 수식에서 s는 복소변수로서 라플라스 연산자(Laplace operator)이며, 적분이 존재하는 범위의 값이다.  함수 f(t)는 0보다 크며(t>0+으로 표현), 연속적이거나 유한개의 불연속점으로 이루어진 조각 또는 부분연속(piecewise continuous)이어야 한다.  여기서 0+의 범위는 적분이 존재하기 위해 함수 f(t)는 0이 아니어야 하므로 0에 무한히 접근한다는 의미이다. 앞으로는 0으로 표현한다. 함수 f(t)는 시간함수이며 f(t)에 대한 라플라스 변환은 e^(-st)의 변수 s와 t에서 시간 t에 대한 적분으로서 s의 함수가 되므로 F(s)로 표현한다.  단위는 시간의 역수가 되어 주파수 단위와 같아지므로 주파수 영역(frequency domain) 또는 함수 F(s)로 표기되는 s-영역(s-domain)이라고 부른다.  t가 0이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환해보면 다음과 같다. \[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \] 계단함수(Step function) 정의 Step function 특정 시점 이후에 일정한 값을 유지하는 함수를 계단함수라 한다. 계단함수 u(t)를 라플라스 정의에 따르면 다음과  같다. \[ \begin{align} L[u(t) &= \int_0^\infty u...
Read more »

15. Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수, 1>ζ> 0

이미지
Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수,  1>ζ>0 역변환된 시간함수로 구한다. 역변된 함수는 아래와 같다. \[ K_p e^{-θs} \left\{\frac{1}{s}-\frac{s+ζω_n}{(s+ζω_n)^2+{ω_d}^2 }-\frac{ζω_n}{ω_d}   \frac{ω_d}{(s+ζω_n)^2+{ω_d}^2}\right\} \] \[→ L^{-1}→\] \[ K_p\cdot f(t-θ)\left\{1-e^{-ζω_n t} cos⁡ω_d  t-\frac{ζω_n}{ω_d} e^{-ζω_n t} sin⁡ω_d t \right\} \] 1>ζ>0, Underdamped인 경우 라플라스와 Z 변환표를 참조하자. \[ δ(n-k)  → Z→ z^{-k} \] \[ 1 → Z→  \frac{1}{1-z^{-1}} \] \[ \begin{align} e^{-akT}  &cos⁡ω kT \ → Z→ \\[12pt] &\frac{1-e^{-aT} z^{-1}  cos⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT}z^{-2}} \end{align} \] \[ \begin{align} e^{-akT}  &sin⁡ω kT \ → Z→  \\[12pt] &\frac{1-e^{-aT} z^{-1} sin⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT} z^{-2}} \end{align} \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}  cos⁡ω kT\)와 \(e^{-akT}  sin⁡ω kT \)의 a는 \(ζω_n\)이고, ω는 \(ω_d\)이다. \[ \begin{align} F(z)=K_p \cdot z^{-θ} &\c...
Read more »