4. Z 변환(Z-transform), 데드 타임 1차 함수와 게인(First order with dead time and gain)

이득을 가진 데드 타임 1차 함수(First order with dead time and gain)의 Z 변환


앞에서 서술한  이득을 가진 데드 타임 1차 함수(First order with dead time and gain)의 라플라스 변환을 Z 변환을 통한 차분 방정식(Difference Equation)을 활용하여 디지털 시스템에 적용해 보자.
Laplace 변환과 Z 변환에서 설명한 전달 함수의 관계에서 이득을 가진 데드 타임 1차 함수를 대입하면 다음과 같다.

\[ \begin{align} F(z) &=Z\left\{(1-z^{-1})\frac{F(s)}{s}\right\} \\[12pt] &=(1-z^{-1})Z\left\{\frac{F(s)}{s}\right\} \\[12pt] &=(1-z^{-1} )Z\left\{ \frac {\frac{K_p e^{-θs}}{1+τs}}{s}\right\} \\[12pt] &=(1-z^{-1} )Z\left\{ \frac{K_p e^{-θs}}{s(1+τs)}\right\} \\[12pt] &=(1-z^{-1})Z\left\{K_p e^{-θs}\frac{1}{τs+1}\frac{1}{s}\right\} \\[12pt] &=(1-z^{-1})Z\left\{K_p e^{-θs} \frac{1}{τ}\frac{1}{s+\frac{1}{τ}}\frac{1}{s}\right\} \end{align} \]

여기서 \( e^{-θs} \)는 \(z^{-k} \)와 같으므로 \( z^{-θ}\)이고, \( K_p\)와 \(\frac{1}{τ}\)은 상수이므로
 
\[ =K_p  \frac{1}{τ} z^{-θ} (1-z^{-1})Z\left\{\frac{1}{s+\frac{1}{τ}}  \frac{1}{s}\right\} \]

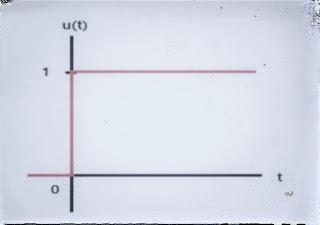
로 나타낼 수 있고, \( \frac{1}{s}\)의 역변환은 \(u(t)\)로서 계단 함수이다.

\[ \begin{align} L[u(t)] &=∫_0^∞ u(t) e^{-st} dt=∫_0^∞ 1\cdot e^{-st} dt \\[12pt] &=\left[\frac{e^{-st}}{-s}\right]_0^∞=\frac{1}{s} \end{align} \]


\[ u(t)=\begin{cases}0 & (t<0) \\ 1 & (t≥0) \end{cases}\]


계단 함수는 위의 정의에 따라

\[ \begin{align} F(z)&=Z[f(k)]=\sum_{k=0}^∞ z^{-k} \\[12pt] &=1+z^{-1}+z^{-2}+⋯ \end{align} \]

으로 나타낼 수 있고, 수열 \( ∑_{k=0}^∞ z^{-k} \)은 

\[ \begin{align} \sum_{k=1}^∞ ar^{k-1} &=a+ar+ar^2+⋯+ar^{n-1}+⋯ \\[12pt] &=\frac{a}{1-r} \end{align} \]

와 같은 등비수열(Geometric sequence) 형태이다. 그러므로 계단 함수의 Z 변환은 다음과 같다.

\[ \begin{align} F(z)&=Z[f(k)]=\sum_{k=0}^∞ z^{-k} \\[12pt] &=1+z^{-1}+z^{-2}+⋯ \\[12pt] &= \frac{1}{1-z^{-1}} \end{align} \]

\( \frac{1}{s+\frac{1}{τ}} \)은 라플라스 변환표에 제시된 \( \frac{1}{s+a}→ L^{-1}→e^{-at} \)에 의해 감쇠(Damping)하는 지수 함수(Polynomial function)이다.

\[ \frac{1}{s+\frac{1}{τ}}→ L^{-1}→e^{-\frac{1}{τ }t} \]

이것의 정의는 다음과 같다.

\[ f(kT)=\begin{cases}e^{-akT} & (k ≥0) \\0 &          (k<0) \end{cases} \]

지수 함수의 Z 변환은 Z 변환 정의에 따라 다음과 같다.

\[ \begin{align} &F(z) =Z[e^{-akT} ]=\sum_{k=0}^{∞} e^{-akT} z^{-k} \\[12pt] &=1+e^{-aT} z^{-1}+e^{-2aT} z^{-2}+e^{-3aT} z^{-3} + ⋯ \\[12pt] &=\frac{1}{1-e^{-aT} z^{-1}} \end{align} \]

즉, \( e^{-\frac{1}{τ}t} \)는 다음과 같다.

\[ F(z)=\frac{1}{1-e^{-\frac{T}{τ}} z^{-1}} \]

위 변환은 라플라스와 Z 변환표에 나와 있는 것과 같다.

\[ δ(n-k)=\begin{cases}1 & (n=k) \\ 0 & (n≠k) \end{cases}→ X(z)→z^{-k} \]

\[ \begin{align} \frac{1}{s}→ &L^{-1}→1(t)  → \\ &x(k)→ 1(k)→ X(z)→  \frac{1}{1-z^{-1}} \end{align} \]

\[ \begin{align} \frac{1}{s+a}&→ L^{-1}→e^{-at} → \\ &x(k)→e^{-akT}→ X(z)→ \frac{1}{1-e^{-aT} z^{-1}} \end{align} \]


변환 과정을 나타내면 다음과 같다.

\[ \begin{align} F(z) &=Z \left\{ (1-z^{-1}) \frac{F(s)}{s} \right\} \\[12pt] &=(1-z^{-1}) Z \left\{ \frac{F(s)}{s} \right\} \\[12pt] &=(1-z^{-1}) Z \left\{ Kp e^{-θs} \frac{1}{τ} \frac{1}{s+\frac{1}{τ}} \frac{1}{s} \right\} \\[12pt] &=Kp \frac{1}{τ} z^{-θ} (1-z^{-1}) Z \left\{ \frac{1}{s+\frac{1}{τ}}  \frac{1}{s} \right\} \\[12pt] &=Kp \frac{1}{τ} z^{-θ} (1-z^{-1}) \left( \frac{1}{1-z^{-1}} \right) Z \left\{ \frac{1}{s+\frac{1}{τ}} \right\} \\[12pt] &=Kp \frac{1}{τ} z^{-θ} (1-z^{-1}) \left(\frac{1}{1-z^{-1}}\right)\left(\frac{1}{1-e^{-\frac{T}{τ}} z^{-1}} \right) \\[12pt] &=Kp  \frac{1}{τ} z^{-θ} \left( \frac{1}{1-e^{-\frac{T}{τ}}  z^{-1}}\right) \\[12pt] &=\left( \frac{\frac{Kp}{τ} z^{-θ}}{1-e^{-\frac{T}{τ}} z^{-1}}\right) \end{align} \]

이것을 차분 방정식 형태로 나타내면 다음과 같다.

\[ \begin{align} F(z)&=\frac{Output(zero-state response)}{Input} \\[12pt] &= \frac{Y(z)}{X(z)} \end{align} \]

\[(Input)Y(z)=(Output)X(z)\]

\[\left(1-e^{-\frac{T}{τ}} z^{-1}\right)Y(z)=\left(\frac{Kp}{τ} z^{-θ}\right)X(z)\]

좌측 수식은 y[k]에 해당하며 y[k]를 기준으로 정리한다.

\[ y[k]=e^{-\frac{T}{τ}} \cdot y[k-1]+\frac{Kp}{τ} \cdot f[k-θ] \]

응답 특성을 살펴보자. Gain=1, θ=0, τ=1, 표본 주기 T=1
 
Z transform period
Z transform period

Z 변환에 의해 생성된 데이터는 표본 주기에 의해 0초, 1초, 2초, 3초, …, 10초에 데이터가 존재한다. 이론적으로 라플라스 역변환은 모든 시간에 데이터를 가지고 있으나 계산을 0.1초 간격으로 풀이하면 0.1초마다 데이터를 가지고 있는 것을 볼 수 있다. 위 그림을 값을 유지하는 실선 형태로 표현하면 아래와 같다. Z 변환은 표본 유지(Sample hold)를 적용한다.
 
Sample and hold
Sample and hold

위와 같이 역변환된 식은 연속적인 그래프로 Z 변환된 식은 표본 주기에 따른 형태로 나타난다. Z 변환된 데이터는 계산된 수식에 의한 데이터로부터 표본 유지를 적용하기 위한 과정을 수행하게 된다. 이때 표본 주기를 역변환의 계산 주기와 동일하게 하면 아래와 같다.
 
Continuous
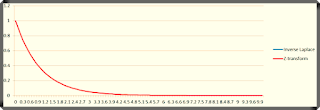Continuous

위의 그림과 같이 Laplace 역변환과 Z 변환을 통한 응답 특성 그래프는 동일하다. 이 둘을 구분하기 위해 Z변환은 세로 막대형으로 그림을 나타내면 아래와 같다.
 
Laplace and Z transform
Laplace and Z transform

Laplace 역변환은 선(Line)으로 Z 변환은 세로 막대형으로 응답특성을 표현 할 수 있다. 연속성은 선으로 세로 막대형은 표본 주기성을 나타낸다. 이와 같이 Laplace 역변환과 Z 변환을 통한 응답 특성은 동일하다. 물론 표본화에 따른 오차가 발생하므로 동일하지는 않다. 다만 이것은 표본 주기를 작게 하면 할수록 작아지며 오차는 줄어 든다.

댓글

댓글 쓰기

이 블로그의 인기 게시물

22. Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임((Integrator with first order and dead time)

이미지
Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임(Integrator with first order and dead time) Integrator with first order and dead time,  Laplace 모델의  Z 변환은 역변환된 시간함수로 구한다. \[ f(t)=f(t-θ)\frac{1}{τ_1} \left(1-e^{-\frac{τ_1}{τ_2}  t}\right) \] 적분과 데드타임으로 이루어진 1차 함수의 Z 변환과 특성 위의 역변환된 시간함수를 라플라스 & Z 변환표를 참조하여 변환한다. \[ δ(n-k)  → Z→ Z^{-k} \] \[ 1(k)  → Z→  \frac{1}{1-z^{-1} } \] \[ e^{-akT}  → Z→  \frac{1}{1-e^{-aT} z^{-1}}  \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}\)의 a는 \(\frac{τ_1}{τ_2}\) T이다. \[ \begin{align} F(z)&= z^{-θ} \frac{1}{τ_1}  \left(\frac{1}{1-z^{-1}}-\frac{1}{1-e^{-\frac{τ_1}{τ_2} T}  z^{-1}}\right)\\[12pt]&= z^{-θ}  \frac{1}{τ_1} \left\{\frac{(1-e^{-\frac{τ_1}{τ_2} T}  z^{-1} )-(1-z^{-1} )}{(1-z^{-1} )(1-e^{-\frac{τ_1}{τ_2}  T}  z^{-1} } \right\}\\[12pt]&= z^{-θ} \frac{1}{τ_1}  \left\{\frac{(-e^{-\frac{τ_1}{τ_2} T}+1) z^{-1}}{1+(-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-1}+e^{-...
Read more »

1. 라플라스 변환과 Z 변환(Laplace transform and Z-transform)

이미지
라플라스 변환 (Laplace transform) 함수 f(t)에 \( e^{-st} \)를 곱해 t=0에서 t=∞까지 t에 대해 적분하였을 때, 적분값이 존재하는 경우에는 s에 관한 함수로 표현되며 s에 대한 새로운 함수를 함수 f(t)의 라플라스 변환(Laplace transform)이라고 한다. 이를 수식으로 표현하면 다음과 같다. \[ F(s)=L[f(t)]=\int_{0+}^\infty e^{-st} f(t)dt \] 수식에서 s는 복소변수로서 라플라스 연산자(Laplace operator)이며, 적분이 존재하는 범위의 값이다.  함수 f(t)는 0보다 크며(t>0+으로 표현), 연속적이거나 유한개의 불연속점으로 이루어진 조각 또는 부분연속(piecewise continuous)이어야 한다.  여기서 0+의 범위는 적분이 존재하기 위해 함수 f(t)는 0이 아니어야 하므로 0에 무한히 접근한다는 의미이다. 앞으로는 0으로 표현한다. 함수 f(t)는 시간함수이며 f(t)에 대한 라플라스 변환은 e^(-st)의 변수 s와 t에서 시간 t에 대한 적분으로서 s의 함수가 되므로 F(s)로 표현한다.  단위는 시간의 역수가 되어 주파수 단위와 같아지므로 주파수 영역(frequency domain) 또는 함수 F(s)로 표기되는 s-영역(s-domain)이라고 부른다.  t가 0이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환해보면 다음과 같다. \[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \] 계단함수(Step function) 정의 Step function 특정 시점 이후에 일정한 값을 유지하는 함수를 계단함수라 한다. 계단함수 u(t)를 라플라스 정의에 따르면 다음과  같다. \[ \begin{align} L[u(t) &= \int_0^\infty u...
Read more »

15. Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수, 1>ζ> 0

이미지
Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수,  1>ζ>0 역변환된 시간함수로 구한다. 역변된 함수는 아래와 같다. \[ K_p e^{-θs} \left\{\frac{1}{s}-\frac{s+ζω_n}{(s+ζω_n)^2+{ω_d}^2 }-\frac{ζω_n}{ω_d}   \frac{ω_d}{(s+ζω_n)^2+{ω_d}^2}\right\} \] \[→ L^{-1}→\] \[ K_p\cdot f(t-θ)\left\{1-e^{-ζω_n t} cos⁡ω_d  t-\frac{ζω_n}{ω_d} e^{-ζω_n t} sin⁡ω_d t \right\} \] 1>ζ>0, Underdamped인 경우 라플라스와 Z 변환표를 참조하자. \[ δ(n-k)  → Z→ z^{-k} \] \[ 1 → Z→  \frac{1}{1-z^{-1}} \] \[ \begin{align} e^{-akT}  &cos⁡ω kT \ → Z→ \\[12pt] &\frac{1-e^{-aT} z^{-1}  cos⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT}z^{-2}} \end{align} \] \[ \begin{align} e^{-akT}  &sin⁡ω kT \ → Z→  \\[12pt] &\frac{1-e^{-aT} z^{-1} sin⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT} z^{-2}} \end{align} \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}  cos⁡ω kT\)와 \(e^{-akT}  sin⁡ω kT \)의 a는 \(ζω_n\)이고, ω는 \(ω_d\)이다. \[ \begin{align} F(z)=K_p \cdot z^{-θ} &\c...
Read more »