5. 라플라스(Laplace), 데드 타임 2차 함수와 이득(Second order with dead time and gain)

라플라스 모델(Laplace model)의 2차 함수(Second order)와 고유 진동수(Natural frequency)와 감쇠비(Damping ratio)



시스템 또는 함수로 나타낸 시스템에서 차수란 전달함수에서 최고차수를 의미한다. Laplace 모델에서는 laplace 연산자인 s의 차수를 의미한다.

감쇠는 시스템에서 외란이 발생한 후 시스템의 진동이 감소하는 것을 나타낸다. 외란은 일종의 입력과 같은 의미이다. 감쇠비 또는 댐핑 비율은 진동의 변화가 변화하는 것을 나타내는 것으로 ζ 로 표시한다. 

ζ의 상태에 따라 시스템의 상태를 나타내는데, ζ=0인 경우에는 undamped, 0<ζ<1인 경우에는 underdamped, ζ=1인 경우에는 critically damped, ζ=1에서 ζ>1인 경우에는 overdamped된 시스템이라고 한다.

라플라스 2차 함수의 일반적인 형태는 다음과 같다.

\[ laplace \ 2차 함수 =  \frac{{ω_n}^{2} }{s^{2} +2ζω_n s+{ω_n}^{2} } \]

\( ω_n \)은 고유 진동수를 나타내며, ζ는 damping ration을 나타낸다.

위 함수에서 이득과 dead time 및 시간상수 또는 시상수(time constant: τ)를 추가하면 다음과 같다.

Gain과 dead time이 추가된 2차 함수
\[ =  \frac{K_p e^{-θs} {ω_n}^2}{s^2+2ζω_n s+{ω_n}^2 } \]

아래와 같은 형태의 2차 전달 함수의 경우를 살펴보자.
 
Second order
Second order

이것을 전달함수로 나타내면 다음과 같다.

\[ \frac{K_p e^{-θs}}{(1+τ_1 s)(1+τ_2 s)} \]

위 함수를 전개하면

\[ \frac{K_P e^{-θs}}{τ_1 τ_2 s^2 +(τ_1+τ_2)s+1 } \]

이처럼 2차 함수로 되어 있으며, damping ratio와 고유진동수 그리고 시상수로 이루어진 함수의 응답특성을 살펴 보자.

Damping ratio ζ와 고유진동수 \(ω_n \)로 이루어진 2차 전달 함수

\[ laplace \ 2차 함수= \frac{K_p e^{-θs} {ω_n}^2}{s^2+2ζω_n s+{ω_n}^2 } \]

전달 함수를 F(s)라 하고 전개한다.

\[ \begin{align} F(s) &= \frac{K_p e^{-θs} {ω_n}^2}{s^2+2ζω_n s+{ω_n}^2 } \\[12pt] &= K_p e^{-θs}\cdot \frac{{ω_n}^2}{s^2+2ζω_n s+{ω_n}^2} \\[12pt] &= K_p e^{-θs}\cdot \frac{{ω_n}^2}{s^2+2ζω_n s+{ω_n}^2+ζ^2 {ω_n}^2-ζ^2 {ω_n}^2}\\[12pt] &= K_p e^{-θs}\cdot \frac{{ω_n}^2}{(s+ζω_n)^2+{ω_n}^2-ζ^2 {ω_n}^2 }\\[12pt] &= K_p e^{-θs}\cdot \frac{{ω_n}^2}{(s+ζω_n)^2+{ω_n}^2 (1-ζ^2)} \end{align} \]

여기서  \( ω_d=ω_n \sqrt{1-ζ^2} \)라하면

\[ {ω_d}^2={ω_n}^2 (1-ζ^2) \]
\[ ω_n=\frac{ω_d}{\sqrt{1-ζ^2} }\]

\( \therefore \)
\[ \begin{align} &= K_p e^{-θs}  \cdot \frac{ \frac{{ω_d}^2}{1-ζ^2}}{(s+ζω_n)^2+{ω_d}^2}\\[12pt] &= K_p e^{-θs} \cdot \frac{ω_d}{(s+ζω_n )^2+{ω_d}^2 }  \cdot \frac{ω_d}{1-ζ^2}\\[12pt] &= K_p e^{-θs}  \cdot \frac{ω_d}{(s+ζω_n )^2+{ω_d}^2 }  \cdot \frac{ω_n \sqrt{1-ζ^2}}{1-ζ^2}  \cdot  \frac{\sqrt{1-ζ^2 }}{\sqrt{1-ζ^2}}\\[12pt] &= K_p e^{-θs}  \cdot \frac{ω_n}{\sqrt{1-ζ^2}} \cdot \frac{ω_d}{(s+ζω_n )^2+{ω_d}^2} \end{align} \] 

라플라스 변환을 하면
\[ \frac{ω}{(s+a)^2+ω^2 }  → L^{-1}→ e^{-at}  sin⁡ω t \]

그러므로 F(s)의 역변환은 다음과 같이 표현 된다.
\[ \begin{align} &K_p e^{-θs}  \cdot \frac{ω_n}{\sqrt{1-ζ^2 )}} \cdot \frac{ω_d}{(s+ζω_n )^2+{ω_d}^2}\\[12pt] &→ L^{-1}→\\[12pt] &K_p \cdot f(t-θ) \cdot \frac{ω_n}{\sqrt{1-ζ^2}}\cdot e^{-ζω_{n}t} sin⁡ ω_n \sqrt{1-ζ^2 } t \end{align} \]

damping ratio ζ와 고유진동수 ω_n로 이루어진 2차 전달 함수의 응답특성은 Gain=1, θ=0, ω_n=2, ζ=0.3일 때 아래와 같다. 

 
Response characteristics Laplace second order and Natural frequency, damping ration
Response characteristics Laplace second order and Natural frequency, damping ration

그래프의 파란색 부분이 응답특성이다. 붉은 색은 감쇄를 나타내고 역변환된 수식에서 지수함수 \( \frac{ω_n}{\sqrt{1-ζ^2}} \cdot e^{-ζω_n t} \)부분으로서 응답특성은 지수곡선을 넘지 않는다.
진동하는 길이는 sin곡선에 의하며 sin 곡선은 역변환 수식에서 sin함수 부분으로 응답특성은 한 주기 (2π)를 sin 주기\( \ ω_n \sqrt{1-ζ^2} \)과 같다. 

고유진동수: ωn 와 damping ratio: ζ가 변경 될 때의 특성은 아래 그림과 같다.
   
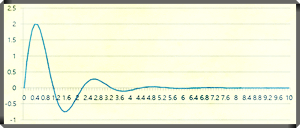Response characteristics Laplace second order, ωn=1, ζ=0.3
Response characteristics Laplace second order, ωn=1, ζ=0.3


Response characteristics Laplace second order, ωn=2, ζ=0.3
Response characteristics Laplace second order, ωn=2, ζ=0.3


Response characteristics Laplace second order, ωn=3, ζ=0.3
Response characteristics Laplace second order, ωn=3, ζ=0.3


Response characteristics Laplace second order, ωn=3, ζ=0.9
Response characteristics Laplace second order, ωn=3, ζ=0.9


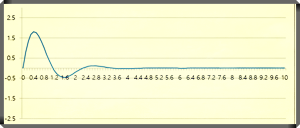Response characteristics Laplace second order, ωn=3, ζ=0.4
Response characteristics Laplace second order, ωn=3, ζ=0.4


Response characteristics Laplace second order, ωn=3, ζ=0.1
Response characteristics Laplace second order, ωn=3, ζ=0.1




2개의 1차 함수가 직렬 연결된 시스템에서 각자 시상수를 가지는 전달함수는 다음과 같다.

\[ \frac{K_p e^{-θs}}{(1+τ_1 s)(1+τ_2 s)} \]

Kp는 시스템 이득(Gain), θ는 dead time, τ1 및 τ2는 시상수(Time constant)

전달함수를 F(s)라 하고 역변환하면 다음과 같다.

\[ \begin{align} F(s) &=\frac{K_p e^{-θs}}{(1+τ_1 s)(1+τ_2 s)}\\[12pt] &=K_P e^{-θs}\frac{1}{1+τ_2 s+τ_1 s+τ_1 τ_2 s^2}\\[12pt] &=K_P e^{-θs}\frac{  1}{τ_1 τ_2 s^2+τ_1 s+τ_2 s+1}\\[12pt] &=K_P e^{-θs}\frac{ 1}{τ_1 τ_2 s^2+s(τ_1+τ_2)+1}\\[12pt] &=K_P e^{-θs}\frac{ \frac{1}{τ_1 τ_2}}{s^2+\frac{1}{τ_1 τ_2} s(τ_1+τ_2)+\frac{1}{τ_1 τ_2}}\\[12pt] &=K_P e^{-θs}\frac{\frac{1}{τ_1 τ_2}}{s^2+\frac{s(τ_1+τ_2)}{τ_1 τ_2}+\frac{1}{τ_1 τ_2}} \end{align} \]

여기서 \( \frac{s(τ_1+τ_2)}{τ_1 τ_2} \)는

 \[ \begin{align} &\frac{s(τ_1+τ_2 )}{τ_1 τ_2 }=s\left( \frac{τ_1+τ_2}{τ_1 τ_2}\right)\\[12pt] &=s\left(\frac{τ_1}{τ_1 τ_2}+\frac{τ_2}{τ_1 τ_2}\right)=s\left(\frac{1}{τ_2}+\frac{1}{τ_1}\right) \end{align} \]
이므로

\[ =K_P\cdot e^{-θs} \cdot \frac{\frac{1}{τ_1 τ_2}}{s^2+s\left(\frac{1}{τ_2} +\frac{1}{τ_1}\right)+\frac{1}{τ_1 τ_2}} \]

라플라스 변환표를 살펴보면 \(\frac{1}{(s+a)(s+b)}\)가 있으며 이를 전개하면 다음과 같다.

\[ \frac{1}{(s+a)(s+b)} =\frac{1}{s^2+s(a+b)+ab}\]

\( \frac{1}{τ1}\)을 a, \(\frac{1}{τ2}\)을 b로 대치하면 라플라스 변환표와 동일하다.

\[ \begin{align} \frac{1}{(s+a)(s+b)} &=\frac{1}{s^2+s(a+b)+ab} \\[12pt] &→ L^{-1}→\\[12pt] &\frac{1}{a-b}(e^{-bt}-e^{-at} )  \end{align} \]

이것은 다음과 같다.

\[ K_P\cdot f(t-θ)\cdot \frac{1}{τ_1  τ_2}\cdot \frac{1}{\frac{1}{τ_2} -\frac{1}{τ_1}}\left( e^{-\frac{1}{τ_1} θ}-e^{-\frac{1}{τ_2}θ} \right) \]

위 식에서 \( \frac{1}{τ_1  τ_2}\cdot \frac{1}{\frac{1}{τ_2} -\frac{1}{τ_1}}\)을 정리해준다.

\[ \begin{align} &\frac{1}{τ_1  τ_2}\cdot \frac{1}{\frac{1}{τ_2} -\frac{1}{τ_1}}=\frac{1}{τ_1  τ_2}\cdot \frac{1}{\frac{τ_1-τ_2}{τ_2  τ_1}}\\[12pt]&=\frac{1}{τ_1  τ_2}\cdot \frac{τ_1 τ_2}{τ_1-τ_2}=\frac{1}{τ_1-τ_2} \end{align} \]

2차 함수 Laplace 모델의 역변환은 다음과 같다.

\[ f(t)=K_P\cdot f(t-θ)\cdot \frac{1}{τ_1-τ_2 }\left(e^{-\frac{θ}{τ_1}}-e^{-\frac{θ}{τ_2}} \right) \]

응답특성은 Gain=4, θ=0, τ1=1, τ2=2일 때 아래와 같다. 
 

Response characteristics Laplace second order
Response characteristics Laplace second order

응답특성 그래프를 살펴보면, 시상수 τ1 과τ2 에 의해 특성이 결정되며, 최고점(최대값)은 각 시상수의 의한 지수 함수 값의 절대차, 이득 및 시상수 차이값을 나눈 값의 절대값의 곱이다. 이때 시상수 τ1 과τ2 은 같지 않다.

\[ K_P\cdot \left|\frac{1}{τ_1-τ_2}\right|\cdot \left|e^{-\frac{θ}{τ_1}}-e^{-\frac{θ}{τ_2}} \right|      \ where\  τ_1≠ τ_2  \]

응답특성의 최고점의 위치는 시상수 τ1 과 τ2 사이에 있다.

\[ τ_1 ≤ \left|e^{-\frac{θ}{τ_1}} -e^{-\frac{θ}{τ_2}} \right| ≤τ_2   \   where \ τ_1≠ τ_2  \]






댓글

댓글 쓰기

이 블로그의 인기 게시물

22. Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임((Integrator with first order and dead time)

이미지
Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임(Integrator with first order and dead time) Integrator with first order and dead time,  Laplace 모델의  Z 변환은 역변환된 시간함수로 구한다. \[ f(t)=f(t-θ)\frac{1}{τ_1} \left(1-e^{-\frac{τ_1}{τ_2}  t}\right) \] 적분과 데드타임으로 이루어진 1차 함수의 Z 변환과 특성 위의 역변환된 시간함수를 라플라스 & Z 변환표를 참조하여 변환한다. \[ δ(n-k)  → Z→ Z^{-k} \] \[ 1(k)  → Z→  \frac{1}{1-z^{-1} } \] \[ e^{-akT}  → Z→  \frac{1}{1-e^{-aT} z^{-1}}  \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}\)의 a는 \(\frac{τ_1}{τ_2}\) T이다. \[ \begin{align} F(z)&= z^{-θ} \frac{1}{τ_1}  \left(\frac{1}{1-z^{-1}}-\frac{1}{1-e^{-\frac{τ_1}{τ_2} T}  z^{-1}}\right)\\[12pt]&= z^{-θ}  \frac{1}{τ_1} \left\{\frac{(1-e^{-\frac{τ_1}{τ_2} T}  z^{-1} )-(1-z^{-1} )}{(1-z^{-1} )(1-e^{-\frac{τ_1}{τ_2}  T}  z^{-1} } \right\}\\[12pt]&= z^{-θ} \frac{1}{τ_1}  \left\{\frac{(-e^{-\frac{τ_1}{τ_2} T}+1) z^{-1}}{1+(-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-1}+e^{-...
Read more »

1. 라플라스 변환과 Z 변환(Laplace transform and Z-transform)

이미지
라플라스 변환 (Laplace transform) 함수 f(t)에 \( e^{-st} \)를 곱해 t=0에서 t=∞까지 t에 대해 적분하였을 때, 적분값이 존재하는 경우에는 s에 관한 함수로 표현되며 s에 대한 새로운 함수를 함수 f(t)의 라플라스 변환(Laplace transform)이라고 한다. 이를 수식으로 표현하면 다음과 같다. \[ F(s)=L[f(t)]=\int_{0+}^\infty e^{-st} f(t)dt \] 수식에서 s는 복소변수로서 라플라스 연산자(Laplace operator)이며, 적분이 존재하는 범위의 값이다.  함수 f(t)는 0보다 크며(t>0+으로 표현), 연속적이거나 유한개의 불연속점으로 이루어진 조각 또는 부분연속(piecewise continuous)이어야 한다.  여기서 0+의 범위는 적분이 존재하기 위해 함수 f(t)는 0이 아니어야 하므로 0에 무한히 접근한다는 의미이다. 앞으로는 0으로 표현한다. 함수 f(t)는 시간함수이며 f(t)에 대한 라플라스 변환은 e^(-st)의 변수 s와 t에서 시간 t에 대한 적분으로서 s의 함수가 되므로 F(s)로 표현한다.  단위는 시간의 역수가 되어 주파수 단위와 같아지므로 주파수 영역(frequency domain) 또는 함수 F(s)로 표기되는 s-영역(s-domain)이라고 부른다.  t가 0이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환해보면 다음과 같다. \[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \] 계단함수(Step function) 정의 Step function 특정 시점 이후에 일정한 값을 유지하는 함수를 계단함수라 한다. 계단함수 u(t)를 라플라스 정의에 따르면 다음과  같다. \[ \begin{align} L[u(t) &= \int_0^\infty u...
Read more »

15. Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수, 1>ζ> 0

이미지
Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수,  1>ζ>0 역변환된 시간함수로 구한다. 역변된 함수는 아래와 같다. \[ K_p e^{-θs} \left\{\frac{1}{s}-\frac{s+ζω_n}{(s+ζω_n)^2+{ω_d}^2 }-\frac{ζω_n}{ω_d}   \frac{ω_d}{(s+ζω_n)^2+{ω_d}^2}\right\} \] \[→ L^{-1}→\] \[ K_p\cdot f(t-θ)\left\{1-e^{-ζω_n t} cos⁡ω_d  t-\frac{ζω_n}{ω_d} e^{-ζω_n t} sin⁡ω_d t \right\} \] 1>ζ>0, Underdamped인 경우 라플라스와 Z 변환표를 참조하자. \[ δ(n-k)  → Z→ z^{-k} \] \[ 1 → Z→  \frac{1}{1-z^{-1}} \] \[ \begin{align} e^{-akT}  &cos⁡ω kT \ → Z→ \\[12pt] &\frac{1-e^{-aT} z^{-1}  cos⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT}z^{-2}} \end{align} \] \[ \begin{align} e^{-akT}  &sin⁡ω kT \ → Z→  \\[12pt] &\frac{1-e^{-aT} z^{-1} sin⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT} z^{-2}} \end{align} \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}  cos⁡ω kT\)와 \(e^{-akT}  sin⁡ω kT \)의 a는 \(ζω_n\)이고, ω는 \(ω_d\)이다. \[ \begin{align} F(z)=K_p \cdot z^{-θ} &\c...
Read more »