20. Z 변환(Z-transform), 적분과 데드타임(Integrator with dead time)


Z 변환(Z-transform), 적분과 데드타임(Integrator with dead time)


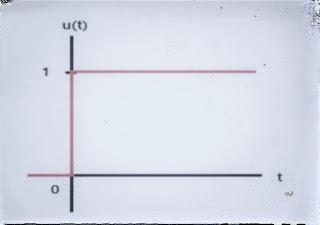
계단 함수(Step function)의 정의를 살펴보자.


\[ f(t)=\begin{cases} 1 & (t≥0) \\ 0 & (t<0) \end{cases} \]


계단함수의 Z 변환은 아래와 같이 표현된다.


\[ \begin{align} F(z)&=Z[f(k)]=\sum_{k=0}^∞ z^{-k}\\[12pt]&=1+z^{-1}+z^{-2}+⋯\\[12pt]&=  \frac{1}{1-z^{-1} } \end{align} \]


계단함수의 Z변환은 아래와 같다.


\[ Z[f(t-nT)]=z^{-n} F(z)\]





적분과 데드타임으로 이루어진 Z 변환 함수의 특성


계단 함수 x(kT)를 1T만큼 지연 시킨 함수 x(k-T)는 아래와 같다.


\[ x(k-T)=\begin{cases}1   & (k≥T) \\ 0   & (k<T) \end{cases} \]

이것을 Z 변환으로 표현하면 다음과 같다.


\[ Z[x(kT-T)]=z^{-1} Z[x(kT)]= \frac{z^{-1}}{1-z^{-1}} \]


시간 지연을 가지는 함수로 표현하자.


\[ \begin{align} L\left(\frac{e^{-θs}}{τS}\right)&=e^{-θs}\cdot \frac{1}{τ}\cdot \frac{1}{s}\\[12pt]&=\frac{1}{τ}\cdot Z[f(kT-θT)\cdot 1(k)]\\[12pt]&=Kp\cdot z^{-θ} Z[1(k)]= \frac{ \frac{1}{τ}\cdot z^{-θ}}{1-z^{-1} } \end{align} \]


차분 방정식 형태로 나타내자.


\[ F(z)=\frac{Output(zero-state response)}{Input}=\frac{Y(z)}{X(z)}\]
\[ (Input)Y(z)=(Output)X(z) \]


\[ (1-z^{-1} )Y(z)=\left(\frac{1}{τ}\cdot z^{-θ} \right)X(z) \]


y[k]를 기준으로 정리하면 다음과 같다.


\[ \begin{align} y[k]&=1\cdot y[k-1]\\[12pt]&+\frac{1}{τ}\cdot f[k-θ] \end{align} \]
 
응답특성을 나타내는 그래프를 살펴보자.



Z-trasnform, Responce graph, Integrator with dead time
Z-trasnform, Responce graph, Integrator with dead time

응답특성 그래프에서 표본주기 T=3, 지연시간 θ=2로, Gain=1, τ=1로 하였다. 


Z 변환으로 얻은 응답특성은 지정된 지연특성보다 1이 늦은 특성을 가지는 시스템이 된다. 이것은 표본화에 따른 오차이다. 표본오차(Sampling error)는 표본주기를 작게 하면 할수록 작아진다.



댓글

댓글 쓰기

이 블로그의 인기 게시물

22. Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임((Integrator with first order and dead time)

이미지
Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임(Integrator with first order and dead time) Integrator with first order and dead time,  Laplace 모델의  Z 변환은 역변환된 시간함수로 구한다. \[ f(t)=f(t-θ)\frac{1}{τ_1} \left(1-e^{-\frac{τ_1}{τ_2}  t}\right) \] 적분과 데드타임으로 이루어진 1차 함수의 Z 변환과 특성 위의 역변환된 시간함수를 라플라스 & Z 변환표를 참조하여 변환한다. \[ δ(n-k)  → Z→ Z^{-k} \] \[ 1(k)  → Z→  \frac{1}{1-z^{-1} } \] \[ e^{-akT}  → Z→  \frac{1}{1-e^{-aT} z^{-1}}  \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}\)의 a는 \(\frac{τ_1}{τ_2}\) T이다. \[ \begin{align} F(z)&= z^{-θ} \frac{1}{τ_1}  \left(\frac{1}{1-z^{-1}}-\frac{1}{1-e^{-\frac{τ_1}{τ_2} T}  z^{-1}}\right)\\[12pt]&= z^{-θ}  \frac{1}{τ_1} \left\{\frac{(1-e^{-\frac{τ_1}{τ_2} T}  z^{-1} )-(1-z^{-1} )}{(1-z^{-1} )(1-e^{-\frac{τ_1}{τ_2}  T}  z^{-1} } \right\}\\[12pt]&= z^{-θ} \frac{1}{τ_1}  \left\{\frac{(-e^{-\frac{τ_1}{τ_2} T}+1) z^{-1}}{1+(-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-1}+e^{-...
Read more »

1. 라플라스 변환과 Z 변환(Laplace transform and Z-transform)

이미지
라플라스 변환 (Laplace transform) 함수 f(t)에 \( e^{-st} \)를 곱해 t=0에서 t=∞까지 t에 대해 적분하였을 때, 적분값이 존재하는 경우에는 s에 관한 함수로 표현되며 s에 대한 새로운 함수를 함수 f(t)의 라플라스 변환(Laplace transform)이라고 한다. 이를 수식으로 표현하면 다음과 같다. \[ F(s)=L[f(t)]=\int_{0+}^\infty e^{-st} f(t)dt \] 수식에서 s는 복소변수로서 라플라스 연산자(Laplace operator)이며, 적분이 존재하는 범위의 값이다.  함수 f(t)는 0보다 크며(t>0+으로 표현), 연속적이거나 유한개의 불연속점으로 이루어진 조각 또는 부분연속(piecewise continuous)이어야 한다.  여기서 0+의 범위는 적분이 존재하기 위해 함수 f(t)는 0이 아니어야 하므로 0에 무한히 접근한다는 의미이다. 앞으로는 0으로 표현한다. 함수 f(t)는 시간함수이며 f(t)에 대한 라플라스 변환은 e^(-st)의 변수 s와 t에서 시간 t에 대한 적분으로서 s의 함수가 되므로 F(s)로 표현한다.  단위는 시간의 역수가 되어 주파수 단위와 같아지므로 주파수 영역(frequency domain) 또는 함수 F(s)로 표기되는 s-영역(s-domain)이라고 부른다.  t가 0이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환해보면 다음과 같다. \[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \] 계단함수(Step function) 정의 Step function 특정 시점 이후에 일정한 값을 유지하는 함수를 계단함수라 한다. 계단함수 u(t)를 라플라스 정의에 따르면 다음과  같다. \[ \begin{align} L[u(t) &= \int_0^\infty u...
Read more »

15. Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수, 1>ζ> 0

이미지
Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수,  1>ζ>0 역변환된 시간함수로 구한다. 역변된 함수는 아래와 같다. \[ K_p e^{-θs} \left\{\frac{1}{s}-\frac{s+ζω_n}{(s+ζω_n)^2+{ω_d}^2 }-\frac{ζω_n}{ω_d}   \frac{ω_d}{(s+ζω_n)^2+{ω_d}^2}\right\} \] \[→ L^{-1}→\] \[ K_p\cdot f(t-θ)\left\{1-e^{-ζω_n t} cos⁡ω_d  t-\frac{ζω_n}{ω_d} e^{-ζω_n t} sin⁡ω_d t \right\} \] 1>ζ>0, Underdamped인 경우 라플라스와 Z 변환표를 참조하자. \[ δ(n-k)  → Z→ z^{-k} \] \[ 1 → Z→  \frac{1}{1-z^{-1}} \] \[ \begin{align} e^{-akT}  &cos⁡ω kT \ → Z→ \\[12pt] &\frac{1-e^{-aT} z^{-1}  cos⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT}z^{-2}} \end{align} \] \[ \begin{align} e^{-akT}  &sin⁡ω kT \ → Z→  \\[12pt] &\frac{1-e^{-aT} z^{-1} sin⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT} z^{-2}} \end{align} \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}  cos⁡ω kT\)와 \(e^{-akT}  sin⁡ω kT \)의 a는 \(ζω_n\)이고, ω는 \(ω_d\)이다. \[ \begin{align} F(z)=K_p \cdot z^{-θ} &\c...
Read more »