19. 라플라스(Laplace), 적분과 데드타임(Integrator with dead time)

라플라스(Laplace), 적분과 데드타임(Integrator with dead time)

적분은 특정 구간에서 함수의 넓이를 구할 때 사용한다. 함수 f(t)에 \(e^{-st}\)를 곱해 0에서 t까지 적분하였을 때 적분 값이 존재하는 경우에 이것을 라플라스 적분 함수라고 하고, s에 관한 함수로 표현한다.

함수 f(x)를 시간 0에서 t까지 적분하는 함수는 다음과 같다.

\[ \int_0^t f(x)  dx=u,  u'=f(t) \]
\[ e^{-st}=v',v= -\frac{1}{s }e^{-st} \]

\[ \int u v'=u v- \int u' v \]

라플라스 정의에 따라 변환하면 다음과 같다.

\[ \begin{align} L\left[\int_0^t f(x)  dx\right]&=\int_0^∞\left[\int_0^t f(x)dx\right]  e^{-st} dt\\[12pt]&=\left[-\frac{1}{s} e^{-st}  \int_0^t f(x) dx\right]_0^\infty - \int_0^∞ \left[-\frac{1}{s} e^{-st} \right]f(t)dt\\[12pt]&=\frac{1}{s} \int_0^∞ f(t) e^{-st} dt=\frac{1}{s} F(s) \end{align} \]

적분과 데드타임 함수의 응답특성

\(\frac{1}{s}\)은 적분 함수로 나타내며, 지연 특성의 dead time과 시상수 형태의 적분 함수는 다음과 같다.

\[ \frac{e^{-θs}}{τs} \]

위의 함수에서 θ는 dead time, τ는 시상수(Time constant)이다.

Dead time θ와 시상수 τ를 가지는 \(\frac{e^{-θs}}{τs}\)는 다음과 같다.

\[ \begin{align} L\left[\frac{1}{τ} u(t-θ)\right]&=\int_0^∞ e^{-st}  \frac{1}{τ} u(t-θ)dt\\[12pt]&=\int_0^θ e^{-st}  0 dt+\int_θ^∞ e^{-st}  \frac{1}{τ} dt\\[12pt]&= -\frac{1}{s} e^{-st}  \frac{1}{τ}\rvert_θ^\infty\\[12pt]&=0-\left(-\frac{1}{s} e^{-sθ}  \frac{1}{τ}\right)\\[12pt]&=\frac{1}{s} e^{-sθ}  \frac{1}{τ}\\[12pt]&=\frac{e^{-θs}}{τs} \end{align} \]

적분과 데드타임 함수의 역변환은 다음과 같다.

\[ f(t)=\frac{1}{τ}u(t-θ) \]

응답특성을 나타내는 그래프를 살펴보자.

 

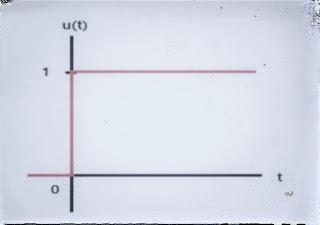
Integrator with dead time, θ=4, τ=1

그래프의 응답특성을 살펴보면 시작점은 0이고 dead time θ만큼 지연된 것을 볼 수 있다. 수렴 값은 시상수에 영향을 받아 \(\frac{1}{τ }\)로 나타난다. 위의 응답특성은 θ=4 만큼 지연되어 발생하고, τ=1에 수렴하는 것을 볼 수 있다.

Dead time θ=6이고 시상수 τ=2이면 응답 특성은 6만큼 지연된 시점에 발생하고 시상수에 따라 반비례한 0.5에 수렴하는 것을 알 수 있다.

Integrator with dead time, θ=6, τ=2