23. 라플라스(Laplace), 역응답 프로세스와 리드 타임(Inverse response process with lead time)


라플라스(Laplace), 역응답 프로세스와 리드 타임(Inverse response process with lead time)


응답특성이 반대의 값으로 나오다가 최종 출력 값으로 수렴하는 것을 역응답(Inverse response)이라고 한다.

Inverse response
Inverse response

그림은 응답특성의 출력이 음으로 나오다가 양의 형태로 변하며 최종 출력값으로 수렴되는 것을 나타난다.



라플라스, 역응답 프로세스와 리드 타임


응답특성이 처음에 최종 출력값의 반대로 나타났다가 최종 출력값으로 수렴하는 것을 역응답(inverse response)이라고 하는데 이와 같은 응답특성을 나타내기 위해서는 전달함수에 리드 타임(lead time)을 포함하는 전달함수로 표현이 가능하다. 리드 타임은 역응답 형태를 결정하는 시간 상수를 말한다. 
Lead time을 포함하여 1차 함수로 나타내면 다음과 같다.

Laplace function with lead time
Laplace function with lead time


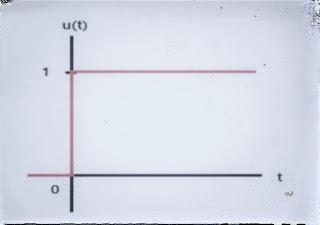
위 식에 계단형태의 응답특성을 위해 계단입력을 적용하여 준다.

Laplace function with lead time multiply step function
Laplace function with lead time multiply step function


여기에 dead time과 시상수를 고려하여 Inverse response process with lead time 의 전달함수를 나타낸다.

Transfer function, Inverse response process with lead time
Transfer function, Inverse response process with lead time


여기서 θ는 dead time, τl은 lead time, τ1, τ2는 시상수(time constant)이다.

이제 위의 식을 역변환(Inverse Laplace transform)하면 다음과 같이 나타낼 수 있다.

Inverse Laplace transform
Inverse Laplace transform


역변환 과정을 알아보자. 제시된 전달함수를 F(s)라 하면

Solution inverse Laplace transform - 1
Solution inverse Laplace transform - 1


위식에서 우측의 수식의 일부를 부분분수(partial fraction)로 전개한다. 

Partial fraction
Partial fraction

A 및 B는 미정계수(undetermined coefficients)로 다음과 같이 구할 수 있다. 

Method of undetermined coefficients - 1
Method of undetermined coefficients - 1

s를 포함하는 항과 일반항으로 분류하여준다.

Method of undetermined coefficients - 2
Method of undetermined coefficients - 2

따라서 

Method of undetermined coefficients - 3
Method of undetermined coefficients - 3

A와 B를 전달함수에 대입한다.

Solution inverse Laplace transform - 2
Solution inverse Laplace transform - 2


라플라스 변환표(Laplace conversion table)를 참조하여, 

Laplace conversion table : No. 1
Laplace conversion table : No. 1

Laplace conversion table : No. 3
Laplace conversion table : No. 3

로 변환된다. 
라플라스 변환표는 블로그 글 13. 라플라스(Laplace) & Z 변환(Z-transform) 변환표(Conversion table)을 참조한다.

따라서 제시된 표준식의 역변환 함수는 다음과 같다.

Inverse Laplace transform.
Inverse Laplace transform.


그러므로 lead time과 시상수에 따라 아래 그림과 같다.
 
Response Lead time graph
Response Lead time graph


Lead time and time constant
Lead time and time constant


1/τ1은 응답특성의 안정화된 값과 관련되어 있고, τl/τ2은 초기값을 결정한다.

τl, τ1, τ2
τl, τ1, τ2


Rise time
Rise time



θ=1, τl=2, τ1=1, τ2=2
θ=1, τl=2, τ1=1, τ2=2

초기값=1, 수렴값=1
 
Response Lead time graph, f(t)
Response Lead time graph, f(t)




θ=1, τl=3, τ1=1, τ2=2
θ=1, τl=3, τ1=1, τ2=2

초기값=1.5, 수렴값=1
 
Response Lead time graph, Up
Response Lead time graph, Up




θ=1, τl=1, τ1=1, τ2=2
θ=1, τl=1, τ1=1, τ2=2

초기값=0.5, 수렴값=1
 
Response Lead time graph, Down
Response Lead time graph, Down




θ=0, τl=-1, τ1=1, τ2=1
θ=0, τl=-1, τ1=1, τ2=1

초기값=-1, 수렴값=1
 
Laplace-Inverse response
Laplace-Inverse response

수렴값은 1/τ1에 의해 1이 되며, 초기값은 τl/τ2에 따라 -1이 되며, 상승시간(63.2%)은 τ(1/τ1)에 의해 결정 된다. 


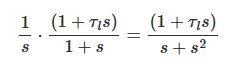
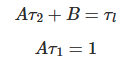
댓글

댓글 쓰기

이 블로그의 인기 게시물

22. Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임((Integrator with first order and dead time)

이미지
Z 변환(Z-transform), 적분과 1차 함수 그리고 데드 타임(Integrator with first order and dead time) Integrator with first order and dead time,  Laplace 모델의  Z 변환은 역변환된 시간함수로 구한다. \[ f(t)=f(t-θ)\frac{1}{τ_1} \left(1-e^{-\frac{τ_1}{τ_2}  t}\right) \] 적분과 데드타임으로 이루어진 1차 함수의 Z 변환과 특성 위의 역변환된 시간함수를 라플라스 & Z 변환표를 참조하여 변환한다. \[ δ(n-k)  → Z→ Z^{-k} \] \[ 1(k)  → Z→  \frac{1}{1-z^{-1} } \] \[ e^{-akT}  → Z→  \frac{1}{1-e^{-aT} z^{-1}}  \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}\)의 a는 \(\frac{τ_1}{τ_2}\) T이다. \[ \begin{align} F(z)&= z^{-θ} \frac{1}{τ_1}  \left(\frac{1}{1-z^{-1}}-\frac{1}{1-e^{-\frac{τ_1}{τ_2} T}  z^{-1}}\right)\\[12pt]&= z^{-θ}  \frac{1}{τ_1} \left\{\frac{(1-e^{-\frac{τ_1}{τ_2} T}  z^{-1} )-(1-z^{-1} )}{(1-z^{-1} )(1-e^{-\frac{τ_1}{τ_2}  T}  z^{-1} } \right\}\\[12pt]&= z^{-θ} \frac{1}{τ_1}  \left\{\frac{(-e^{-\frac{τ_1}{τ_2} T}+1) z^{-1}}{1+(-e^{-\frac{τ_1}{τ_2}  T}+1) z^{-1}+e^{-...
Read more »

1. 라플라스 변환과 Z 변환(Laplace transform and Z-transform)

이미지
라플라스 변환 (Laplace transform) 함수 f(t)에 \( e^{-st} \)를 곱해 t=0에서 t=∞까지 t에 대해 적분하였을 때, 적분값이 존재하는 경우에는 s에 관한 함수로 표현되며 s에 대한 새로운 함수를 함수 f(t)의 라플라스 변환(Laplace transform)이라고 한다. 이를 수식으로 표현하면 다음과 같다. \[ F(s)=L[f(t)]=\int_{0+}^\infty e^{-st} f(t)dt \] 수식에서 s는 복소변수로서 라플라스 연산자(Laplace operator)이며, 적분이 존재하는 범위의 값이다.  함수 f(t)는 0보다 크며(t>0+으로 표현), 연속적이거나 유한개의 불연속점으로 이루어진 조각 또는 부분연속(piecewise continuous)이어야 한다.  여기서 0+의 범위는 적분이 존재하기 위해 함수 f(t)는 0이 아니어야 하므로 0에 무한히 접근한다는 의미이다. 앞으로는 0으로 표현한다. 함수 f(t)는 시간함수이며 f(t)에 대한 라플라스 변환은 e^(-st)의 변수 s와 t에서 시간 t에 대한 적분으로서 s의 함수가 되므로 F(s)로 표현한다.  단위는 시간의 역수가 되어 주파수 단위와 같아지므로 주파수 영역(frequency domain) 또는 함수 F(s)로 표기되는 s-영역(s-domain)이라고 부른다.  t가 0이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환해보면 다음과 같다. \[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \] 계단함수(Step function) 정의 Step function 특정 시점 이후에 일정한 값을 유지하는 함수를 계단함수라 한다. 계단함수 u(t)를 라플라스 정의에 따르면 다음과  같다. \[ \begin{align} L[u(t) &= \int_0^\infty u...
Read more »

15. Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수, 1>ζ> 0

이미지
Z 변환(Z-transform), Underdamped, Damping ratio와 고유진동수로 이루어진 2차 전달함수,  1>ζ>0 역변환된 시간함수로 구한다. 역변된 함수는 아래와 같다. \[ K_p e^{-θs} \left\{\frac{1}{s}-\frac{s+ζω_n}{(s+ζω_n)^2+{ω_d}^2 }-\frac{ζω_n}{ω_d}   \frac{ω_d}{(s+ζω_n)^2+{ω_d}^2}\right\} \] \[→ L^{-1}→\] \[ K_p\cdot f(t-θ)\left\{1-e^{-ζω_n t} cos⁡ω_d  t-\frac{ζω_n}{ω_d} e^{-ζω_n t} sin⁡ω_d t \right\} \] 1>ζ>0, Underdamped인 경우 라플라스와 Z 변환표를 참조하자. \[ δ(n-k)  → Z→ z^{-k} \] \[ 1 → Z→  \frac{1}{1-z^{-1}} \] \[ \begin{align} e^{-akT}  &cos⁡ω kT \ → Z→ \\[12pt] &\frac{1-e^{-aT} z^{-1}  cos⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT}z^{-2}} \end{align} \] \[ \begin{align} e^{-akT}  &sin⁡ω kT \ → Z→  \\[12pt] &\frac{1-e^{-aT} z^{-1} sin⁡ω T}{1-2e^{-aT} z^{-1} cos⁡ω T+e^{-2aT} z^{-2}} \end{align} \] δ(n-k)에서 횟수 n은 시간 t이고, 지연횟수 k는 지연시간 θ이고, \(e^{-akT}  cos⁡ω kT\)와 \(e^{-akT}  sin⁡ω kT \)의 a는 \(ζω_n\)이고, ω는 \(ω_d\)이다. \[ \begin{align} F(z)=K_p \cdot z^{-θ} &\c...
Read more »