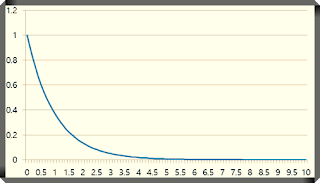
7. Z 변환(Z-transform), 데드 타임 2차 함수와 이득, 시상수(Second order with dead time and gain, Time constant)

2차 전달 함수에서 시상수로 이루어진 경우를 살펴보자. 시상수로 이루어진 2차 함수의 Z 변환은 Laplace 변환과 Z 변환에서 설명한 전달함수의 관계에 2차 함수를 대입하여 구할 수 있다. \[ \begin{align} F(z)&=Z\left\{(1-z^{-1})\frac{F(s)}{s}\right\}=(1-z^{-1})Z\left\{\frac{F(s)}{s}\right\}\\[12pt] &=(1-z^{-1} )Z\left\{ \frac{\frac{K_p e^{-θs}}{(1+τ_1 s)(1+τ_2 s)}}{s}\right\}\\[12pt]&=(1-z^{-1})Z\left\{ \frac{K_pe^{-θs}}{s(1+τ_1 s)(1+τ_2 s)}\right\}\\[12pt]&=(1-z^{-1})Z\left\{K_pe^{-θs}\frac{1}{(1+τ_1 s)(1+τ_2 s)}\frac{1}{s}\right\} \end{align} \] 여기서 \(e^{-θs}\)는 \(z^{-k}\)와 같으므로 \( z^{-θ}\)이고, \(K_p\)는 상수이다. \[=K_p z^{-θ}(1-z^{-1})Z\left\{\frac{1}{(1+τ_1 s)(1+τ_2 s)}\frac{1}{s}\right\} \] \(\frac{1}{s}\)은 라플라스 & Z-변환표를 참조하여 정리한다. \[ \begin{align} &=K_p z^{-θ}(1-z^{-1})\left( \frac{1}{1-z^{-1}}\right)Z\left\{\frac{1}{(1+τ_1 s)(1+τ_2 s)}\right\}\\[12pt] &=K_p z^{-θ}Z\left\{\frac{1}{τ_1 τ_2 s^2+τ_1 s+τ_2 s+1}\right\}\\[12pt] &=K_p z^{-θ} Z\left\{\frac{\frac{1}{τ_1 τ_2 }}{s^2+\frac{τ_1 s}{τ_1 τ_2}+\frac{τ_2 s}{τ_1 τ_2 }...