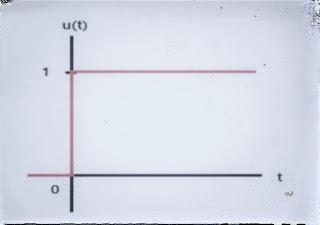
2. 이득을 가지는 데드 타임(Dead time with gain)과 라플라스(Laplace) & Z 변환(Z-transform)

데드 타임과 이득( Dead time with gain) 데드 타임(Dead time) Dead time은 입력에 따라 출력이 변하는 시스템에서 입력 시점에서 출력 시점까지, 입력 변화에 따른 출력 변화가 나타나기까지 시간이 걸리는데 이 지연되는 시간을 데드 타임이라고 한다. 이러한 시스템을 모델로 만들 때 지연 특성(time shift, delay time)을 반영하고 이것을 수식으로 표현하면 아래와 같이 나타낼 수 있다. \[ K_{p} e^{-\theta s} \] Kp는 시스템 이득 또는 프로세스 이득(Gain)이고 θ는 데드 타임이다. 데드 타임의 라플라스 모델 위의 식을 Laplace 모델로서 시간에 대한 함수로 표현하면 \[ f(t) = K_p L(e^{(-\theta s)}) = K_p \cdot f(t-\theta) \] 여기에서 \( L(e^{(-\theta s)} ) \)의 L( )은 괄호 안의 수식이 Laplace 영역(domain)이다. 그리고 우변 항의 \( K_p \)는 시스템 이득을 나타낸다. \( e^{(-\theta s)} \)는 지연 특성을 나타내는 것으로 \( f(t-\theta) \)로 표현할 수 있다. 이것은 연결된 함수를 θ만큼 이동한 것으로 그림으로 표현하면 아래와 같다. 지연 특성 이 함수는 \[ g(t) = \begin{cases} 0 & \ (t < \theta) \\ f(t-\theta) & \ (t\ge \theta) \end{cases} \] 으로 정의된다. 이것을 변환하면 \[ \begin{align} L[g(t)] &= \int_0^\infty e^{-st}g(t)dt \\[10pt] &= \int_0^\theta e^{-st}g(t)dt + \int_\theta^\infty e^{-st}g(t)dt \end{align} \] 우변 항의 0에서 θ구간은 0이고, θ에서 ∞구간은 \( f(t-\theta)\)이다. \[ \begi...