mathema

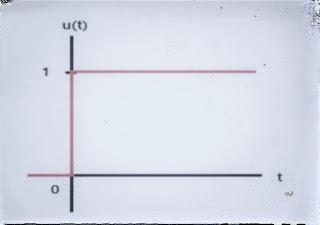
라플라스 변환 (Laplace transform) 함수 f(t)에 \( e^{-st} \)를 곱해 t=0에서 t=∞까지 t에 대해 적분하였을 때, 적분값이 존재하는 경우에는 s에 관한 함수로 표현되며 s에 대한 새로운 함수를 함수 f(t)의 라플라스 변환(Laplace transform)이라고 한다. 이를 수식으로 표현하면 다음과 같다. \[ F(s)=L[f(t)]=\int_{0+}^\infty e^{-st} f(t)dt \] 수식에서 s는 복소변수로서 라플라스 연산자(Laplace operator)이며, 적분이 존재하는 범위의 값이다.  함수 f(t)는 0보다 크며(t>0+으로 표현), 연속적이거나 유한개의 불연속점으로 이루어진 조각 또는 부분연속(piecewise continuous)이어야 한다.  여기서 0+의 범위는 적분이 존재하기 위해 함수 f(t)는 0이 아니어야 하므로 0에 무한히 접근한다는 의미이다. 앞으로는 0으로 표현한다. 함수 f(t)는 시간함수이며 f(t)에 대한 라플라스 변환은 e^(-st)의 변수 s와 t에서 시간 t에 대한 적분으로서 s의 함수가 되므로 F(s)로 표현한다.  단위는 시간의 역수가 되어 주파수 단위와 같아지므로 주파수 영역(frequency domain) 또는 함수 F(s)로 표기되는 s-영역(s-domain)이라고 부른다.  t가 0이상일 때 1의 값을 가지는 함수 u(t)가 있을 때 이를 라플라스 함수로 변환해보면 다음과 같다. \[ u(t) = \begin{cases} 0 & \ (t<0) \\ 1 & \, \, (t \ge 0) \end{cases} \] 계단함수(Step function) 정의 Step function 특정 시점 이후에 일정한 값을 유지하는 함수를 계단함수라 한다. 계단함수 u(t)를 라플라스 정의에 따르면 다음과  같다. \[ \begin{align} L[u(t) &= \int_0^\infty u...